Perímetro:
O Perímetro é a medida do comprimento de um contorno, ou seja é a soma das medidas dos lados de um polígono.Observe um campo de futebol, o perímetro dele é o seu contorno que está de vermelho.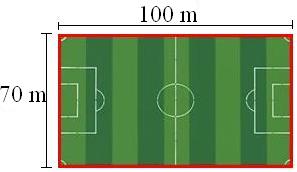
Pra fazermos o cálculo do perímetro devemos somar todos os seus lados:
P = 100 + 70 + 100 + 70
P = 340 m
Outro exemplo:
O perímetro da figura é a soma de todos os seus lados:
P = 10 + 8 + 3 + 1 + 2 + 7 + 2 +3
P = 18 + 4 + 9 + 5
P = 22 + 14
P = 36
OBS: A unidade de medida utilizada no cálculo do perímetro é a mesma unidade de medida de comprimento: metro, centímetro, quilômetro…
Àrea:
A Área é a região plana interna delimitada pelos lados de um polígono. Tal conceito é amplamente usado no dia-a-dia, como na medição de um terreno, na delimitação de um espaço, entre outros. O valor da área de um polígono varia de acordo com seu formato.Cada polígono tem uma forma peculiar para calcular sua área. Exemplificaremos alguns conhecidos, tais como: retângulo, quadrado, paralelogramo, triângulo, trapézio, losango e círculo.Retângulo

Já sabemos que o retângulo possui dois lados iguais chamados de base e outros dois lados iguais chamados de altura. Para sabermos o valor da área de um retângulo (A), devemos multiplicar a medida da base (b) pela medida da altura (h).
A = b x h
Quadrado

No quadrado, podemos aplicar o mesmo raciocínio usado para calcular a área do retângulo, multiplicando a medida da base pela medida da altura, mas, como no quadrado a medida de todos os lados é igual (l):
A = l x l ou A = l²
Paralelogramo

Se observarmos a figura ao lado, podemos notar que o paralelogramo é semelhante a um retângulo com os lados inclinados. Se tirarmos uma das partes inclinadas do paralelogramo e a enxertarmos no outro lado, formaremos um retângulo. Assim, a área do paralelogramo é calculado da mesma forma da área do retângulo, ou seja, multiplica-se o valor da base (b) pelo valor da altura (h).
A = b x h
Triângulo
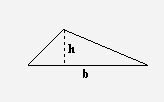
No caso do triângulo, pode-se notar que ele é exatamente metade de um retângulo, portanto, num retângulo cabem dois triângulos, ambos de mesma área. Por conseguinte, a área do triângulo é metade da área do retângulo, ou seja:
A = b x h / 2
Losango

Ao traçar as diagonais, maior (D) e menor (d) do losango, o dividimos em quatro triângulos de áreas iguais, onde cada um tem a oitava parte da área do retângulo de base igual ao valor da diagonal menor do losango e de alura igual ao valor da diagonal maior. Logo, a área do losango é igual a quatro vezes a área de um dos quatro triânglos, resultando na metade da área desse retângulo. Portanto:
A = D x d / 2
Trapézio

Dado um trapézio, como o da figura ao lado, contendo a base menor (b), a base maior (B) e a altura (h). Se ao lado desse trapézio colocarmos um segundo trapézio, idêntico ao primeiro, mas invertido, ou seja, sua base menor voltada para cima e sua base menor voltada para baixo, formaremos um paralelogramo de base igual à soma das bases do trapézio e de mesma altura do trapézio. Assim, encontramos a área desse paralelogramo multiplicando sua base pela altura. Note que o valor achado é igual a área dos dois trapézios idênticos. Portanto, para calcular a área do trapézio, basta dividir o valor encontrado para a área do paralelogramo.
A = [(B + b) x h] / 2
Círculo

Considere um círculo de raio r. Divida-o em várias partes iguais, corte-o de forma que os pedaços sejam de formato triangular e abra a figura, formando um retângulo de base igual a 2x(pi)x r e altura igual ao próprio raio r do círculo. Portanto a área desse retângulo é achada multiplicando sua base pela altura. Deve-se notar que a área desse retângulo é o dobro da área do círculo, sendo assim, acha-se a área do círculo dividindo a área do retângulo por 2.
A = (pi) x r²
Volume:
Volume de um sólido é a quantidade de espaço que esse sólido ocupa. Nesse cálculo, temos que ressaltar as três dimensões do sólido, observando o seu formato. O entendimento de volume é usado, mesmo que intuitivamente, em nossas ações no dia-a-dia, por exemplo: antes de estacionar um carro, calculamos mentalmente o espaço do carro e verificamos se tal espaço é compatível com as dimensões do carro, ao instalar uma TV em um móvel, conferimos, primeiro, se o espaço disponível pode comportar a TV, entre outros exemplos.Alguns sólidos geométricos são formados por polígonos e esses polígonos recebem o nome de faces do polígono. Já o segmento que une duas faces do polígono recebe o nome de aresta do sólido. Assim como no cálculo da área, o cálculo do volume de um sólido depende do formato do sólido. Mas, de forma geral, o volume de um sólido geométrico é calculado a partir do produto de sua base por sua altura. Por enquanto, calcularemos o volume de alguns sólidos, como: o paralelepípedo retângulo, o cubo e o cilindro.
Paralelepípedo Retângulo

O paralelepípedo retângulo é um sólido cujas seis faces são retângulos. Para calcular o volume do paralelepípedo retângulo é necessário fazer o produto da área de sua base pela altura. Mas, como a base do paralelepípedo retângulo tem o formato retangular, exprimimos o valor de sua área por b x c. Portanto, se multiplicarmos o valor da área da base pela altura (a) do paralelepípedo retângulo, acharemos o valor do volume (V) desse sólido:
V = a x b x c
Cubo

O cubo é um sólido geométrico cujas seis faces são quadrados de mesmo lado. Para calcular o volume do cubo é necessário fazer o produto da área de sua base pela altura. Mas, como a base do cubo é um quadrado de lado a, o valor de sua área é, então, definido pelo lado ao quadrado (a²). Sendo assim, se multiplicarmos o valor da área da base pela altura (a) do cubo, acharemos o valor do volume (V) desse sólido:
V = a x a x a ou V = a³
Cilindro

Cilindro é um sólido geométrico que pode ser entendido como um círculo prolongado até uma altura h. O cilindro possui duas faces iguais e de formato circular. Para calcular o volume do cilindro, deve-se fazer o produto da área de sua base pela altura. No caso do cilindro, sua base é um círculo, portanto a área de sua base é igual a (pi) x r². Multiplicando esse valor pela altura (h) do cilindro, achamos o seu volume (V):
V = (pi) x r² x h
Agora vamos prática com exercícios de área e perímetro clique aqui.


Me ajudou pakas! valeeu rsrs :p
ResponderExcluirverdd
ExcluirToma safada toma safada minha pika entrando em vc
ExcluirDébora safada
ExcluirMuito bom... Bem explicativo e simples de se entender. Me ajudou bastante! Obrigado (=
ResponderExcluirmuito obrigado me ajudou bastante explima mt bem!
ResponderExcluirPow Me Ajudou Bastante ,, Obrigado !
ResponderExcluirvlw mim ajudou bastante
ResponderExcluirgostei muito
ResponderExcluirHum, Muito bacana a explicação.
ResponderExcluirPara calcular o perímetro em outras formas de medidas como km , dam,dm .......... Tem q " somar " também?
ResponderExcluirSim, mas antes vc tem que iguala as unidade de medidas...
Excluirmuito obrigad pela materia disponivel e mais valia
ResponderExcluirÓtimo valeu mesmo, agente grava as formulas sem decorar, simplesmente aprendendo.
ResponderExcluirAjudou muito. Obrigada!!!
ResponderExcluirbrigado /0/
ResponderExcluirMe ajudou bastante.....Obrigada!!!! :)
ResponderExcluirvou fazer bem o teste
ResponderExcluirMuito bom o material me ajudou muito
ResponderExcluirmt bom me ajudou tirei 10 em minha prova
ResponderExcluirAdoreiii, sensacional! PARABÉNS!!!!
ResponderExcluirarea e perimetro sao a mesma coisa ?
ResponderExcluirarea e perimetro sao a mesma coisa ?
ResponderExcluirNão, perimetro é a soma dos lados. Área é a multiplicação da base e a altura
ExcluirNão, perimetro é a soma dos lados do solído. Área é a multiplicação da base e a altura
ResponderExcluire muito bom este site me ajudou muito
ResponderExcluirmuito bom
ResponderExcluirMuito bom, obrigado! ^^
ResponderExcluirmuito bom pra quem vai ter prova amanha
ResponderExcluircomo eu kkkk
muito bom pra quem vai ter prova amanha
ResponderExcluircomo eu kkkk
muuuuuuuuuuuuuuiiiiiiiiiiiiiiiiiiiiiiiiiiiitttttttttttttttttttttttttttttttttttttooooooooooooooooooooooooooo......................
ResponderExcluirobrigado issso me ajudou muito parabens pra que fez essa postagem...
muuuuuuuuuuuuuuiiiiiiiiiiiiiiiiiiiiiiiiiiiitttttttttttttttttttttttttttttttttttttooooooooooooooooooooooooooo......................
ResponderExcluirobrigado issso me ajudou muito parabens pra que fez essa postagem...
muito bom,bem facil de se entender,me ajudou muito.
ResponderExcluirfaz mais mano agora faz de angulos e triangulos agradecido
ExcluirAJUDOU MUITO !!!!!
ResponderExcluirtenho uma duvida aqui Clóvis pertente fazer o calçamento de uma área retangular cuja a largura mede 5,7 m e o comprimento de 7,2 m. sera utilizado nesse calçamento um piso de forma quadra de lado de 30 cm. a área sombreada nesse calçamento corresponde a:
ResponderExcluira)20,52rcm 2
b)15,39rcm2
c)10,26rcm2
d)5,13r cm2
quem sabe me explica isso... sere muito agardecida
de qual quer forma me manda resposta no meu gmail que é: f.patrciamartinelli29@gmail.com.
Obrigada..
Patricia
Muito obrigado :)
ResponderExcluirMuito Bom valeu a ajuda!!!
ResponderExcluirEste comentário foi removido por um administrador do blog.
ResponderExcluirMelhor site de matemática que já vi.
ResponderExcluirExcelente artigo. Bem objetivo, compreendi minhas dúvidas. Obrigada.
ResponderExcluirobrigado
ResponderExcluirMelhor explicação que eu já vi
ResponderExcluirCom isso vou poder colar na prova bjsss <3
ResponderExcluirMuito bom vey!!!Meus parabéns a quem fez essa postagem!
ResponderExcluirGostei bastante, explica muito bem. SUPER ÚTIL, porem, fiquei com uma duvida, o que é " PI " e como " calculá-lo " ?
ResponderExcluirPi é aproximadamente 3,14, bons estudos!!
ExcluirPi é 3,14
ExcluirGOSTEI
ResponderExcluiradorei muito obrigado
ResponderExcluirOla pesoas
ResponderExcluirvlw. ajudo muito.to aqui pq eu to de recuperação final
ResponderExcluir7°ano e to estudando, fui vlw........
passei
ExcluirObrigada ! Ajudou muito explicado de forma simples e clara.
ResponderExcluirMachista
ExcluirMuito obrigado, me ajudou bastante...
ResponderExcluirNa área tem q se multiplicar a base pela altura?
ResponderExcluirmuito bom me ajudou bastante nas minhas duvidas
ResponderExcluirconcerteza irei bem na prova!
muito bom me ajudou bastante nas minhas duvidas
ResponderExcluirconcerteza irei bem na prova!
me ajudou muito, amanha tenho prova de matemática , agora estou salva kk <3
ResponderExcluirEste comentário foi removido por um administrador do blog.
ResponderExcluirNão entendi as medidas da figura: Altura de um lado é 10 cm e a soma das alturas do lado oposto é 3cm + 2cm + 2cm = 7cm A soma da base é 8cm + 1cm = 9cm o lado oposto 7cm+ 3cm = 10 cm
ResponderExcluirTive a mesma dúvida, porém, se as medidas estiverem certas, teremos dois quadrados menores e um trapézio (centro-maior)ou um polígono irregular, já que não há referências de ângulos retos na figura. Mas o exemplo foi usado para cálculo do perímetro e não da área, certo? Então, qualquer inferência aqui é desnecessária.
Excluirmano o cara so esta ensinando se faz melhor cria um site e fassa sua coisa e nao vem falar das coisas dos outros entao deixa o cara ensina
ExcluirEu não entendi foi é nada tentei fazer um cálculo mas olha o cabeça dura de se entendeer
ResponderExcluirMuito obrigado ajudou muito
ResponderExcluirPara uma pesquisa e explicativo ajuda para curiosidades, eu recomendaria👍🏻👍🏻👍🏻✌🏻️
ResponderExcluirGostei bastante aprendi muitas coisas que não sabia
ResponderExcluirObrigado me ajudou muito parabéns aí em!!👏👏❤
ResponderExcluirMe ajudou bastante eu estava desesperada por isso obg melhor site vou divulgar agora para as minhas amigas que também estão a procura de um bom site pra ajudá-las PARABÉNS realmente ❤❤��
ResponderExcluirMe ajudou muito
ResponderExcluirMuito bom ensina muito bem :)
ResponderExcluirMe ajudou muito bastante
ResponderExcluirE apenas esses objetos que possuem voleme?
ResponderExcluir🤗🤗🤗Adorei! Me ajudou muito nas revisões do conteúdo de matemática para o concurso. Valeu! 🤗🤗🤗🤗
ResponderExcluirCadê a resposta
ResponderExcluirEu não consegui fazer nada
ResponderExcluir